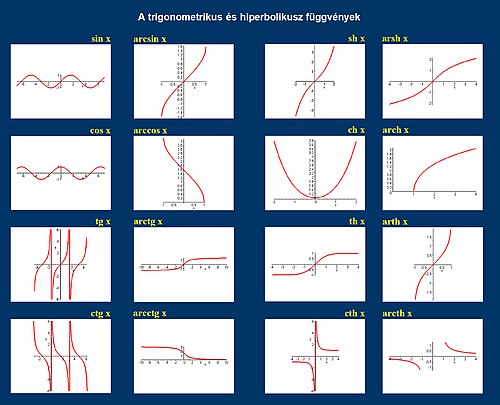
A trigonometrikus függvények vagy szögfüggvények eredetileg egy derékszögű háromszög egy szöge és két oldalának hányadosa közötti összefüggést írják le (innen nyerték magyar és latin nevüket is). A szögfüggvények fontosak többek között a geometriai számításoknál, különféle mozgások (harmonikus rezgőmozgás, körmozgás) és a periodikus jelenségek leírásánál, és a műszaki élet számtalan területén.

A szögfüggvények a derékszögű háromszög két oldalának hányadosa és a szög összefüggésén kívül az egységsugarú körben tekintett forgásszög-végpontok metszeteivel (vetületeivel, koordinátáival) is definiálhatók. Ez utóbbi definíció már 90°, azaz π/2-nél nagyobb, sőt, negatív (mindent összevéve, tetszőleges valós) argumentumokra is működik.

A matematikai analízis eredményei szerint a szögfüggvények végtelen sorként vagy bizonyos differenciálegyenletek megoldásaként is meghatározhatóak. Ily módon már komplex számokra is értelmezhetőek. Mindezeket alább bemutatjuk.

Hagyományosan hat fontos szögfüggvény alakult ki (ezek közül négyet használnak gyakrabban, de csak kettő tekinthető igazán alapvetőnek, a többi ezekből racionális műveletekkel kapható), melyeket az alábbi táblázat tartalmaz. A korai függvénytáblák más szögfüggvényeket is használtak, ilyen például a verszinusz (1 ‒ cos θ) és az exszekáns (sec θ ‒ 1), de ezeket manapság aligha használják.

A szögfüggvények általánosíthatók más γ alapszögekre is. Ezek definiálhatók γ szögű háromszög, és ferdeszögű koordináta-rendszer segítségével is, ahol az egységvektorok hajlásszöge π-γ. Eszerint a γ alapszög még további általánosítás esetén sem lehet π egész számú többszöröse.

Függvény	Rövidítés	Összefüggés
Szinusz	sin	${\displaystyle \sin \alpha =\cos \left({\frac {\pi }{2}}-\alpha \right)\,}$
Koszinusz	cos	${\displaystyle \cos \alpha =\sin \left({\frac {\pi }{2}}-\alpha \right)\,}$
Tangens	tg (vagy tan)	${\displaystyle {\rm {{tg}\;\alpha ={\frac {\sin \alpha }{\cos \alpha }}={\rm {{ctg}\;\left({\frac {\pi }{2}}-\alpha \right)={\frac {1}{\rm {{ctg}\;\alpha }}}\,}}}}}$
Kotangens	ctg (vagy cot)	${\displaystyle {\rm {{ctg}\;\alpha ={\frac {\cos \alpha }{\sin \alpha }}={\rm {{tg}\;\left({\frac {\pi }{2}}-\alpha \right)={\frac {1}{\rm {{tg}\;\alpha }}}\,}}}}}$
Szekáns	sec	${\displaystyle \sec \alpha ={\frac {1}{\cos \alpha }}=\csc \left({\frac {\pi }{2}}-\alpha \right)\,}$
Koszekáns	csc (vagy cosec)	${\displaystyle \csc \alpha ={\frac {1}{\sin \alpha }}=\sec \left({\frac {\pi }{2}}-\alpha \right)\,}$

A szögfüggvények jellemzése

Értelmezési tartomány

A szinusz és a koszinusz az egész számegyenesen értelmezett folytonos függvények. A tangens szakadási helyei π/2+kπ, a kotangensé kπ alakúak. A szekáns minden π/2+kπ, a koszekáns minden kπ pontban szakad.

Értékkészlet

A szinusz és a koszinusz korlátos függvények, értékkészletük a intervallum. A tangens és a kotangens az összes valós számot felveszi. A szekáns és a koszekáns értékkészletéből hiányzik a (-1,1) intervallum.

Szimmetria

A szögfüggvények periodikusak. A szinusz, a koszinusz, a szekáns és a koszekáns periódusa 2π, a tangensé és a kotangensé π.

A szögfüggvények páros vagy páratlan függvények. A szinusz, a tangens, a kotangens és a koszekáns páratlan, a koszinusz és a szekáns páros függvény.

A szögfüggvények menete

A szinusz menete: az első negyedben nő, a másodikban és harmadik csökken, a negyedikben ismét nő. A koszinusz az első és a második negyedben csökken, a harmadikban és a negyedikben nő. A tangens minden (π/2-kπ, π/2+kπ) intervallumon nő, a kotangens minden (kπ, (k+1)π) intervallumon csökken. A szekáns az első és a második negyedben nő, a harmadikban és a negyedikben csökken. A koszekáns az első negyedben csökken, a másodikban és a harmadikban nő, a negyedikben csökken.

Konvexitás

A szinusz az első két negyedben konkáv, a második kettőben konvex. A koszinusz az első negyedben konkáv, a másodikban és a harmadikban konvex, a negyedikben konkáv. A tangens és a kotangens az első negyedben konvex, a másodikban konkáv, a harmadikban konvex, a negyedikben konkáv. A szekáns az első negyedben konvex, a másodikban és a harmadikban konkáv, a negyedikben konvex. A koszekáns az első két negyedben konvex, a második kettőben konkáv.

Nevezetes pontok

A szinusznak nullhelyei vannak a kπ alakú helyeken. Ezek egyben inflexiós pontok is. Maximumhelyei a π/2+2kπ, minimumhelyei a -π/2+2kπ alakú pontok.

A koszinusz a nullát a π/2+kπ helyeken veszi fel. A 2kπ pontokban maximuma, a π+2kπ pontokban minimuma van.

A tangens nullhelyei a kπ, pólushelyei a π/2+kπ pontok. A kotangens a nullát a π/2+kπ veszi fel; a kπ helyeken pólusa van. Nullhelyeik egyben inflexiós pontok is.

A szekáns helyi minimumai a 2kπ, helyi maximumai a kπ+2kπ alakú pontok, a π/2+2kπ helyeken pólusa van.

A koszekáns helyi minimumát az 1/2π+2kπ, helyi maximumát a -1/2π+2kπ helyeken veszi fel; a kπ helyeken pólusa van.

Definíció a derékszögű háromszögben

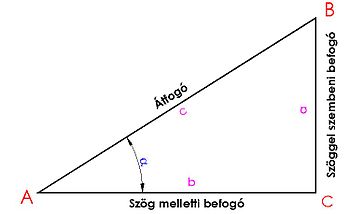
Az α szög szögfüggvényeinek definiálásához vegyünk fel egy tetszőleges ABC derékszögű háromszöget, melynek A csúcspontjában mérhető az α szög. A háromszög oldalai a következők:

• az átfogó a derékszöggel szemben lévő (leghosszabb) oldal, c-vel jelöljük,
• a szöggel szembeni oldal a szóban forgó szöggel átellenes oldal, jelölése a,
• a szög melletti oldal a szóban forgó szög mellett lévő oldal (a szög egyik szára), jelölése b.

A vizsgált háromszög az euklideszi síkban fekszik, tehát a háromszög szögeinek összege π radián (vagy 180°) és két nem derékszögű szöge nulla és π/2 radián között van. A derékszögű háromszögben a szögfüggvények csak ebben a tartományban értelmezhetők. Később a definíciót az egységsugarú kör segítségével kiterjesztjük az összes valós számra.

1) Egy szög szinusza a szöggel szembeni befogó és az átfogó hányadosa

${\displaystyle \sin \alpha ={\frac {\hbox{szöggel szemközti befogó}}{\hbox{átfogó}}}={\frac {a}{c}}.}$

Megjegyzendő, hogy a fenti összefüggés minden olyan derékszögű háromszögre igaz, melynek egyik szöge α, mivel minden ilyen háromszög hasonló egymáshoz.

2) Egy szög koszinusza a szög melletti oldal és az átfogó hányadosa. Esetünkben:

${\displaystyle \cos \alpha ={\frac {\hbox{szög melletti befogó}}{\hbox{átfogó}}}={\frac {b}{c}}.}$

3) Egy szög tangense a szöggel szembeni oldal és a szög melletti oldal hányadosa:

${\displaystyle {\rm {tg}}\;\alpha ={\frac {\hbox{szöggel szemközti befogó}}{\hbox{szög melletti befogó}}}={\frac {a}{b}}.}$

A többi három szögfüggvényt a fenti függvényekkel definiálhatjuk.

4) A koszekáns csc(α) a sin(α) reciproka, vagyis az átfogó és a szöggel szembeni befogó hányadosa:

${\displaystyle \csc \alpha ={\frac {\hbox{átfogó}}{\hbox{szöggel szemközti befogó}}}={\frac {c}{a}}.}$

5) A szekáns sec(α) a cos(α) reciproka, azaz az átfogó és a szög melletti befogó hányadosa:

${\displaystyle \sec \alpha ={\frac {\hbox{átfogó}}{\hbox{szög melletti befogó}}}={\frac {c}{b}}.}$

6) A kotangens ctg(α) a tg(α) reciproka, azaz a szög melletti és a szöggel szemben lévő befogó hányadosa:

${\displaystyle {\rm {ctg}}\;\alpha ={\frac {\hbox{szög melletti befogó}}{\hbox{szöggel szemközti befogó}}}={\frac {b}{a}}.}$

Definíció az egységsugarú kör ill. az egységvektor segítségével

A hat szögfüggvény az egységsugarú kör segítségével is meghatározható. Ez a definíció lehetővé teszi, hogy a szögfüggvényeket ne csak a 0 és π/2 radián (0°-90°) szögtartományra értelmezzük, hanem kiterjesszük az összes pozitív és negatív szögre (valós értékre). Az egységsugarú kör ugyanakkor könnyen használható vizuális segédeszköz is a szögfüggvényeket értelmező összes derékszögű háromszög megmutatására.

A képen néhány nevezetes szög van feltüntetve radiánban mérve. A kör középpontjától jobbra húzott egyenes jelenti a 0 radián szöget. A pozitív szögek másik szára ettől az óramutató járásával ellenkező irányban, míg a negatív szögek másik szára az óramutató járásával megegyező irányban helyezkednek el. A kör középpontjában vegyünk fel egy derékszögű koordináta-rendszert. Ha felrajzolunk egy derékszögű háromszöget, melynek egyik befogója az x tengelyre esik, egyik csúcspontja a középpontban van, átfogója egységnyi, vagyis az egységsugarú kör sugara és a középpontban lévő szög α, akkor az átfogó kör kerületére eső pontjának x koordinátája cos α, y koordinátája pedig sin α lesz. Mivel az átfogó egyenlő a sugárral és így hossza egységnyi, írható: sin α = y/1 és cos α = x/1.

2π-nél nagyobb vagy -2π-nél kisebb szögek esetén a szög szára tovább folytathatja elfordulását a középpont körül. Így látható, hogy a szinusz- és koszinuszfüggvény 2π szerint periodikus függvény:

${\displaystyle \sin \alpha =\sin \left(\alpha +2\pi k\right)}$

${\displaystyle \cos <!--\; \; -->}$Információ forrás: https://hu.wikipedia.org/wiki/Koszinusz
A lap szövege Creative Commons Nevezd meg! – Így add tovább! 3.0 licenc alatt van; egyes esetekben más módon is felhasználható. Részletekért lásd a felhasználási feltételeket.

---